Intro to NNs: MNIST
Content for this tutorial has been modified from content originally written by:
Marieme Ngom, Bethany Lusch, Asad Khan, Prasanna Balaprakash, Taylor Childers, Corey Adams, Kyle Felker, and Tanwi Mallick
Getting Started
This tutorial will serve as a gentle introduction to neural networks and deep learning through a hands-on classification problem using the MNIST dataset.
In particular, we will introduce neural networks and how to train and improve their learning capabilities. We will use the PyTorch Python library.
The MNIST dataset contains thousands of examples of handwritten numbers, with each digit labeled 0-9.
[2025-08-04 23:22:01,582514][I][ezpz/__init__:265:ezpz] Setting logging level to 'INFO' on 'RANK == 0'
[2025-08-04 23:22:01,584493][I][ezpz/__init__:266:ezpz] Setting logging level to 'CRITICAL' on all others 'RANK != 0'
The MNIST dataset
We will now download the dataset that contains handwritten digits. MNIST is a popular dataset, so we can download it via the PyTorch library.
Note:
xis for the inputs (images of handwritten digits)yis for the labels or outputs (digits 0-9)- We are given “training” and “test” datasets.
- Training datasets are used to fit the model.
- Test datasets are saved until the end, when we are satisfied with our model, to estimate how well our model generalizes to new data.
Note that downloading it the first time might take some time.
The data is split as follows:
- 60,000 training examples, 10,000 test examples
- inputs: 1 x 28 x 28 pixels
- outputs (labels): one integer per example
MNIST data loaded: train=48000 examples validation=12000 examples test=10000 examples input shape=torch.Size([1, 28, 28])Let’s take a closer look. Here are the first 10 training digits:
pltsize = 1
# plt.figure(figsize=(10*pltsize, pltsize))
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.axis("off")
# x, y = training_data[i]
# plt.imshow(x.reshape(28, 28), cmap="gray")
# x[0] is the image, x[1] is the label
plt.imshow(numpy.reshape(training_data[i][0], (28, 28)), cmap="gray")
plt.title(f"{training_data[i][1]}")Generalities:
To train our classifier, we need (besides the data):
- A model that depend on parameters \mathbf{\theta}. Here we are going to use neural networks.
- A loss function J(\mathbf{\theta}) to measure the capabilities of the model.
- An optimization method.
Linear Model
Let’s begin with a simple linear model: linear regression, like last week.
We add one complication: each example is a vector (flattened image), so the “slope” multiplication becomes a dot product. If the target output is a vector as well, then the multiplication becomes matrix multiplication.
Note, like before, we consider multiple examples at once, adding another dimension to the input.
The linear layers in PyTorch perform a basic xW + b.
These “fully connected” layers connect each input to each output with some weight parameter.
We wouldn’t expect a simple linear model f(x) = xW+b directly outputting the class label and minimizing mean squared error to work well - the model would output labels like 3.55 and 2.11 instead of skipping to integers.
We now need:
- A loss function J(\theta) where \theta is the list of parameters (here W and b). Last week, we used mean squared error (MSE), but this week let’s make two changes that make more sense for classification:
- Change the output to be a length-10 vector of class probabilities (0 to 1, adding to 1).
- Cross entropy as the loss function, which is typical for classification. You can read more here.
- An optimization method or optimizer such as the stochastic gradient descent (sgd) method, the Adam optimizer, RMSprop, Adagrad etc. Let’s start with stochastic gradient descent (sgd), like last week. For far more information about more advanced optimizers than basic SGD, with some cool animations, see https://ruder.io/optimizing-gradient-descent/ or https://distill.pub/2017/momentum/.
- A learning rate. As we learned last week, the learning rate controls how far we move during each step.
class LinearClassifier(nn.Module):
def __init__(self):
super().__init__()
# First, we need to convert the input image to a vector by using
# nn.Flatten(). For MNIST, it means the second dimension 28*28 becomes 784.
self.flatten = nn.Flatten()
# Here, we add a fully connected ("dense") layer that has 28 x 28 = 784 input nodes
# (one for each pixel in the input image) and 10 output nodes (for probabilities of each class).
self.layer_1 = nn.Linear(28 * 28, 10)
def forward(self, x):
x = self.flatten(x)
x = self.layer_1(x)
return xLearning
Now we are ready to train our first model.
A training step is comprised of:
- A forward pass: the input is passed through the network
- Backpropagation: A backward pass to compute the gradient \frac{\partial J}{\partial \mathbf{W}} of the loss function with respect to the parameters of the network.
- Weight updates \mathbf{W} = \mathbf{W} - \alpha \frac{\partial J}{\partial \mathbf{W}} where \alpha is the learning rate.
How many steps do we take?
- The batch size corresponds to the number of training examples in one pass (forward + backward).
- A smaller batch size allows the model to learn from individual examples but takes longer to train.
- A larger batch size requires fewer steps but may result in the model not capturing the nuances in the data.
- The higher the batch size, the more memory you will require.
- An epoch means one pass through the whole training data (looping over the batches). Using few epochs can lead to underfitting and using too many can lead to overfitting.
- The choice of batch size and learning rate are important for performance, generalization and accuracy in deep learning.
def train_one_epoch(dataloader, model, loss_fn, optimizer):
model.train()
for batch, (X, y) in enumerate(dataloader):
# forward pass
pred = model(X)
loss = loss_fn(pred, y)
# backward pass calculates gradients
loss.backward()
# take one step with these gradients
optimizer.step()
# resets the gradients
optimizer.zero_grad()def evaluate(dataloader, model, loss_fn):
# Set the model to evaluation mode - some NN pieces behave differently during training
# Unnecessary in this situation but added for best practices
model.eval()
size = len(dataloader.dataset)
num_batches = len(dataloader)
loss, correct = 0, 0
# We can save computation and memory by not calculating gradients here - we aren't optimizing
with torch.no_grad():
# loop over all of the batches
for X, y in dataloader:
pred = model(X)
loss += loss_fn(pred, y).item()
# how many are correct in this batch? Tracking for accuracy
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
loss /= num_batches
correct /= size
accuracy = 100 * correct
return accuracy, loss%%time
epochs = 5
train_acc_all = []
val_acc_all = []
for j in range(epochs):
train_one_epoch(train_dataloader, linear_model, loss_fn, optimizer)
# checking on the training loss and accuracy once per epoch
acc, loss = evaluate(train_dataloader, linear_model, loss_fn)
train_acc_all.append(acc)
print(f"Epoch {j}: training loss: {loss}, accuracy: {acc}")
# checking on the validation loss and accuracy once per epoch
val_acc, val_loss = evaluate(val_dataloader, linear_model, loss_fn)
val_acc_all.append(val_acc)
print(f"Epoch {j}: val. loss: {val_loss}, val. accuracy: {val_acc}")Epoch 0: training loss: 0.5018792031606039, accuracy: 87.63333333333333
Epoch 0: val. loss: 0.49411888864446196, val. accuracy: 87.725
1: training loss: 0.4217252082824707, accuracy: 89.01875
Epoch 1: val. loss: 0.412469542089929, val. accuracy: 88.94166666666666
2: training loss: 0.38779040312767027, accuracy: 89.6875666666666
Epoch 2: val. loss: 0.37800481852064743, val. accuracy: 89.525666
3: training loss: 0.3678283305168152, accuracy: 90.11458333333333
Epoch 3: val. loss: 0.3578848899044889, val. accuracy: 89.9533333
4: training loss: 0.3542445518175761, accuracy: 90.43541666666667
Epoch 4: val. loss: 0.3443203260923954, val. accuracy: 90.28333333333333
CPU times: user 10.8 s, sys: 868 ms, total: 11.7 s
Wall time: 11.3 s# Visualize how the model is doing on the first 10 examples
pltsize = 1
plt.figure(figsize=(10 * pltsize, pltsize))
linear_model.eval()
batch = next(iter(train_dataloader))
predictions = linear_model(batch[0])
for i in range(10):
plt.subplot(1, 10, i + 1)
plt.axis("off")
plt.imshow(batch[0][i, 0, :, :], cmap="gray")
plt.title("%d" % predictions[i, :].argmax())Exercise: How can you improve the accuracy? Some things you might consider: increasing the number of epochs, changing the learning rate, etc.
Prediction
Let’s see how our model generalizes to the unseen test data.
Test loss: 0.33246213272213937, test accuracy: 90.86999999999999We can now take a closer look at the results.
Let’s define a helper function to show the failure cases of our classifier.
def show_failures(model, dataloader, maxtoshow=10):
model.eval()
batch = next(iter(dataloader))
predictions = model(batch[0])
rounded = predictions.argmax(1)
errors = rounded != batch[1]
print(f"Showing max {maxtoshow} first failures.")
print("The predicted class is shown first and the correct class in parentheses.")
ii = 0
plt.figure(figsize=(maxtoshow, 1))
for i in range(batch[0].shape[0]):
if ii >= maxtoshow:
break
if errors[i]:
plt.subplot(1, maxtoshow, ii + 1)
plt.axis("off")
plt.imshow(batch[0][i, 0, :, :], cmap="gray")
plt.title("%d (%d)" % (rounded[i], batch[1][i]))
ii = ii + 1Here are the first 10 images from the test data that this small model classified to a wrong class:
Multilayer Model
Our linear model isn’t enough for high accuracy on this dataset. To improve the model, we often need to add more layers and nonlinearities.
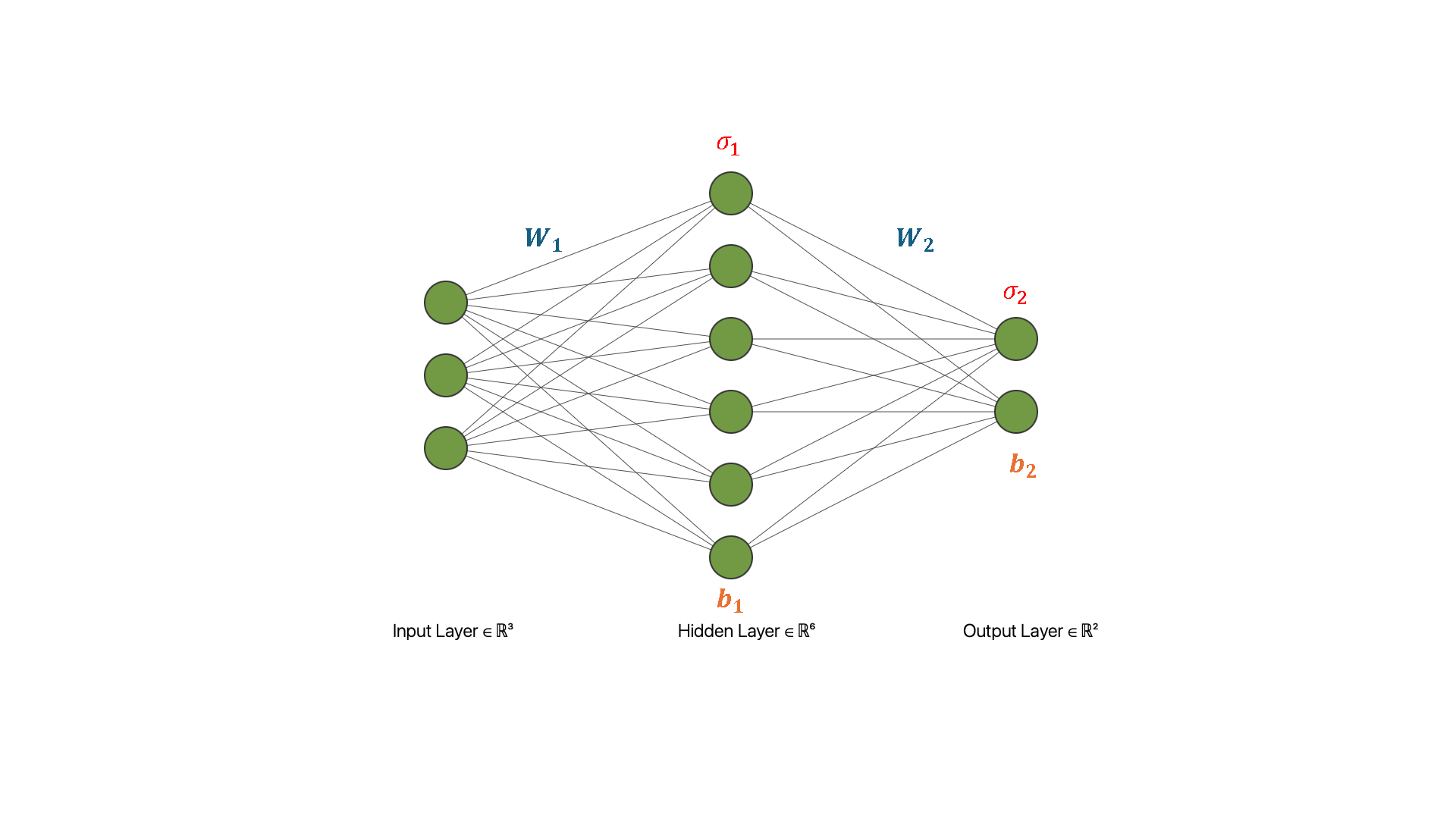
The output of this NN can be written as
\begin{equation} \hat{u}(x) = \sigma_2(\sigma_1(\mathbf{x}\mathbf{W}_1 + \mathbf{b}_1)\mathbf{W}_2 + \mathbf{b}_2), \end{equation}
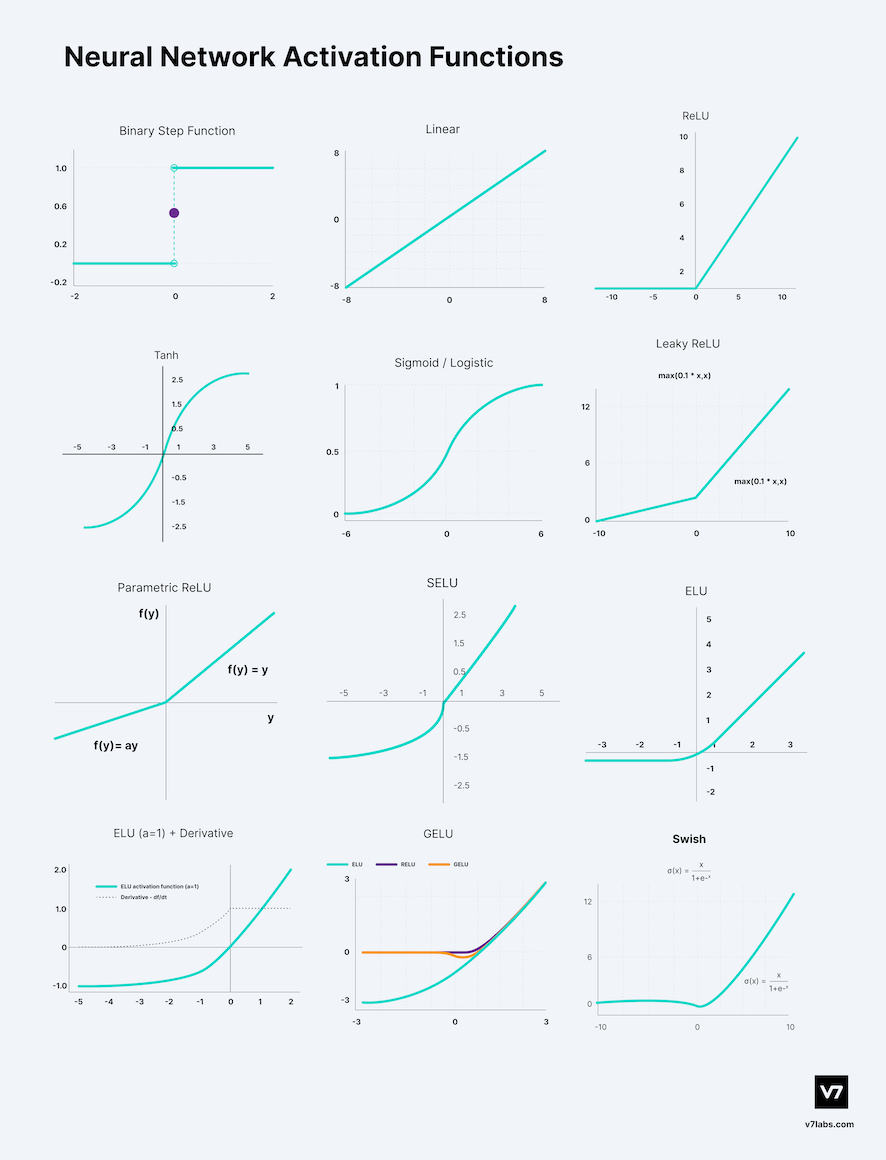
where \mathbf{x} is the input, \mathbf{W}_j are the weights of the neural network, \sigma_j the (nonlinear) activation functions, and \mathbf{b}_j its biases. The activation function introduces the nonlinearity and makes it possible to learn more complex tasks. Desirable properties in an activation function include being differentiable, bounded, and monotonic.
Image source: PragatiBaheti
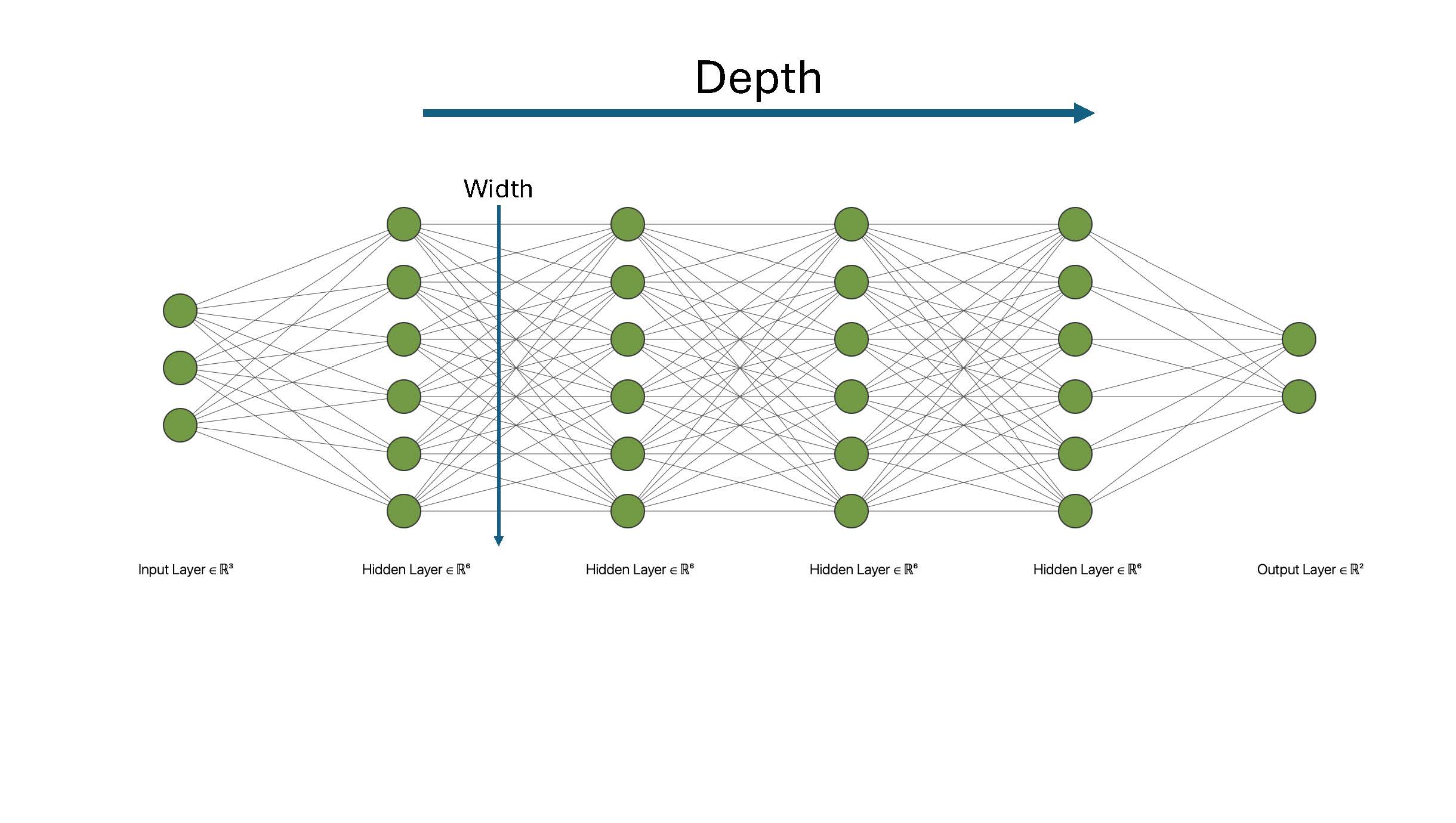
Adding more layers to obtain a deep neural network:
Important things to know
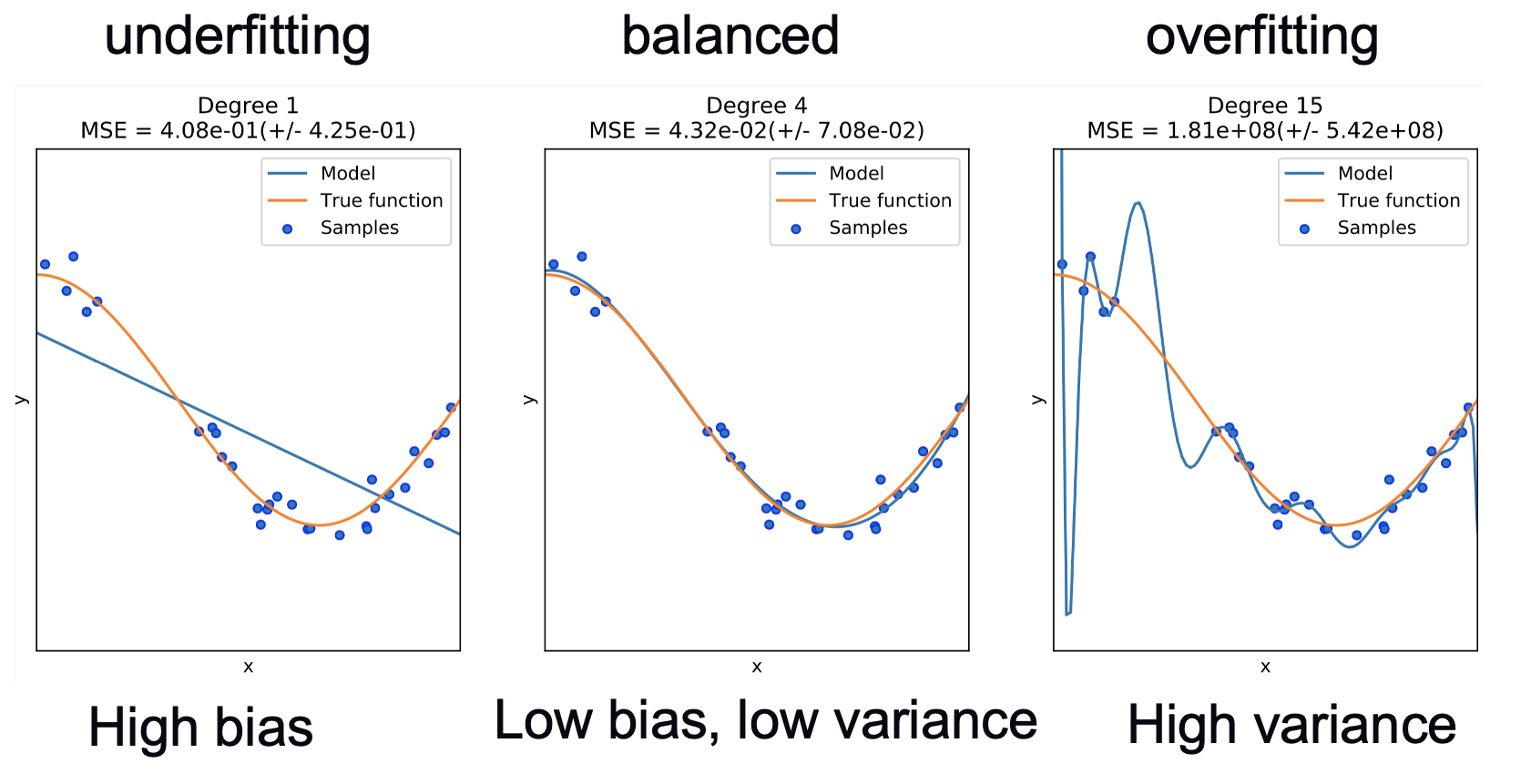
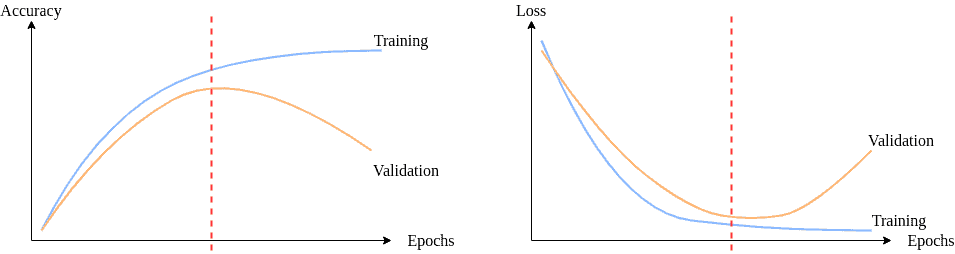
Deep Neural networks can be overly flexible/complicated and “overfit” your data, just like fitting overly complicated polynomials:
Vizualization wrt to the accuracy and loss (Image source: Baeldung):
To improve the generalization of our model on previously unseen data, we employ a technique known as regularization, which constrains our optimization problem in order to discourage complex models.
- Dropout is the commonly used regularization technique. The Dropout layer randomly sets input units to 0 with a frequency of rate at each step during training time, which helps prevent overfitting.
- Penalizing the loss function by adding a term such as \lambda ||\mathbf{W}||^2 is alsp a commonly used regularization technique. This helps “control” the magnitude of the weights of the network.
- Vanishing gradients
- Gradients become small as they propagate backward through the layers.
- Squashing activation functions like sigmoid or tanh could cause this.
- Exploding gradients
- Gradients grow exponentially usually due to “poor” weight initialization.
We can now implement a deep network in PyTorch.
nn.Dropout() performs the Dropout operation mentioned earlier:
# For HW: cell to change activation
class NonlinearClassifier(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.layers_stack = nn.Sequential(
nn.Linear(28 * 28, 50),
nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(50, 50),
nn.ReLU(),
# nn.Dropout(0.2),
nn.Linear(50, 50),
nn.ReLU(),
# nn.Dropout(0.2),
nn.Linear(50, 10),
)
def forward(self, x):
x = self.flatten(x)
x = self.layers_stack(x)
return x%%time
epochs = 5
train_acc_all = []
val_acc_all = []
for j in range(epochs):
train_one_epoch(train_dataloader, nonlinear_model, loss_fn, optimizer)
# checking on the training loss and accuracy once per epoch
acc, loss = evaluate(train_dataloader, nonlinear_model, loss_fn)
train_acc_all.append(acc)
print(f"Epoch {j}: training loss: {loss}, accuracy: {acc}")
# checking on the validation loss and accuracy once per epoch
val_acc, val_loss = evaluate(val_dataloader, nonlinear_model, loss_fn)
val_acc_all.append(val_acc)
print(f"Epoch {j}: val. loss: {val_loss}, val. accuracy: {val_acc}")Epoch 0: training loss: 0.8711661319732666, accuracy: 75.1875
Epoch 0: val. loss: 0.8697689403878882, val. accuracy: 74.55833333333334
1: training loss: 0.4198738198677699, accuracy: 88.297916666666674
Epoch 1: val. loss: 0.4143052941307108, val. accuracy: 88.45833333333334
2: training loss: 0.3039622515439987, accuracy: 91.302083333333334
Epoch 2: val. loss: 0.2973113705186134, val. accuracy: 91.33333334
3: training loss: 0.2426262723406156, accuracy: 93.02291666666666
Epoch 3: val. loss: 0.23850328285009303, val. accuracy: 92.86666666666666
4: training loss: 0.19915112743775049, accuracy: 94.241666666666676
Epoch 4: val. loss: 0.1988548755328706, val. accuracy: 94.11666666666667
CPU times: user 11.7 s, sys: 833 ms, total: 12.6 s
Wall time: 12.4 sRecap
To train and validate a neural network model, you need:
- Data split into training/validation/test sets,
- A model with parameters to learn
- An appropriate loss function
- An optimizer (with tunable parameters such as learning rate, weight decay etc.) used to learn the parameters of the model.
Homework
- Compare the quality of your model when using different:
- batch sizes
- learning rates
- activation functions
- Bonus: What is a learning rate scheduler?
If you have time, experiment with how to improve the model.
Note: training and validation data can be used to compare models, but test data should be saved until the end as a final check of generalization.
Homework solution
Make the following changes to the cells with the comment “#For HW”
#####################To modify the batch size##########################
batch_size = 32 # 64, 128, 256, 512
# The dataloader makes our dataset iterable
train_dataloader = torch.utils.data.DataLoader(training_data, batch_size=batch_size)
val_dataloader = torch.utils.data.DataLoader(validation_data, batch_size=batch_size)
##############################################################################
##########################To change the learning rate##########################
optimizer = torch.optim.SGD(
nonlinear_model.parameters(), lr=0.01
) # modify the value of lr
##############################################################################
##########################To change activation##########################
###### Go to https://pytorch.org/docs/main/nn.html#non-linear-activations-weighted-sum-nonlinearity for more activations ######
class NonlinearClassifier(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.layers_stack = nn.Sequential(
nn.Linear(28 * 28, 50),
nn.Sigmoid(), # nn.ReLU(),
nn.Dropout(0.2),
nn.Linear(50, 50),
nn.Tanh(), # nn.ReLU(),
# nn.Dropout(0.2),
nn.Linear(50, 50),
nn.ReLU(),
# nn.Dropout(0.2),
nn.Linear(50, 10),
)
def forward(self, x):
x = self.flatten(x)
x = self.layers_stack(x)
return x
##############################################################################Bonus question: A learning rate scheduler is an essential deep learning technique used to dynamically adjust the learning rate during training. This strategic can significantly impact the convergence speed and overall performance of a neural network. See below on how to incorporate it to your training.
nonlinear_model = NonlinearClassifier()
loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(nonlinear_model.parameters(), lr=0.1)
# Step learning rate scheduler: reduce by a factor of 0.1 every 2 epochs (only for illustrative purposes)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=2, gamma=0.1)%%time
epochs = 6
train_acc_all = []
val_acc_all = []
for j in range(epochs):
train_one_epoch(train_dataloader, nonlinear_model, loss_fn, optimizer)
#step the scheduler
scheduler.step()
# print the current learning rate
current_lr = optimizer.param_groups[0]['lr']
print(f"Epoch {j+1}/{epochs}, Learning Rate: {current_lr}")
# checking on the training loss and accuracy once per epoch
acc, loss = evaluate(train_dataloader, nonlinear_model, loss_fn)
train_acc_all.append(acc)
print(f"Epoch {j}: training loss: {loss}, accuracy: {acc}")
# checking on the validation loss and accuracy once per epoch
val_acc, val_loss = evaluate(val_dataloader, nonlinear_model, loss_fn)
val_acc_all.append(val_acc)
print(f"Epoch {j}: val. loss: {val_loss}, val. accuracy: {val_acc}")Epoch 1/6, Learning Rate: 0.1
Epoch 0: training loss: 0.35453774413218103, accuracy: 89.84791666666668
val. loss: 0.3428567706346512, val. accuracy: 89.88333333333334
Epoch 2/6, Learning Rate: 0.01000000000000000289.88333333333334
1: training loss: 0.25014649585510296, accuracy: 92.55624999999999
Epoch 1: val. loss: 0.24179457187155884, val. accuracy: 92.60000000000001
3/6, Learning Rate: 0.010000000000000002accuracy: 92.60000000000001
Epoch 2: training loss: 0.23025922616074482, accuracy: 93.25416666666668
val. loss: 0.22265068178375563, val. accuracy: 93.18333333333332
Epoch 4/6, Learning Rate: 0.001000000000000000293.18333333333332
3: training loss: 0.223550607226789, accuracy: 93.43125332
Epoch 3: val. loss: 0.2162884232501189, val. accuracy: 93.30000000000001
5/6, Learning Rate: 0.0010000000000000002curacy: 93.30000000000001
Epoch 4: training loss: 0.22177774112671614, accuracy: 93.43125001
val. loss: 0.21469855186343192, val. accuracy: 93.45833333333333
Epoch 6/6, Learning Rate: 0.000100000000000000033.45833333333333
5: training loss: 0.22121808264404536, accuracy: 93.456253
Epoch 5: val. loss: 0.2141772210597992, val. accuracy: 93.44166666666666
CPU times: user 17.7 s, sys: 3.28 s, total: 20.9 s
Wall time: 19.1 sCitation
@online{foreman2025,
author = {Foreman, Sam and Foreman, Sam and Ngom, Marieme and Zheng,
Huihuo and Lusch, Bethany and Childers, Taylor},
title = {Intro to {NNs:} {MNIST}},
date = {2025-07-17},
url = {https://saforem2.github.io/hpc-bootcamp-2025/01-neural-networks/1-mnist-ipynb/},
langid = {en}
}